Числа, с которыми мы втречаемся в повседневной жизни делятся на несколько видов: положительные, отрицательные, целые, дробные и другие. Если вы умеете определять к какому виду относится то или иное число, то эту страницу можете пропустить. Но если с этим имеются затруднения, то данную тему пропускать не стоит! Дело в том, что дальше, при изучении алгебры мы будем выполнять над числами различные операции: складывать, умножать, делить, вычитать, возводить в степень, брать от них косинус, синус, тангенс, котангенс, логарифм и так далее. И чтобы научиться выполнять эти операции над числами, нужно знать отличие между ними! Например, правила сложения положительных и отрицательных чисел разные. Но мы даже не сможем найти эти правила, если не знаем, какие числа рассматриваются в нашем примере. Поэтому, не стоит начинать дальнейшее изучение алгебры, без знания чисел!

Целые числа: ▼

Состоят из:

• Натуральных чисел
• Числа ноль
• Целых отрицательных чисел

Дробные числа: ▼

Состоят из:

• Дробных положительных чисел
• Дробных отрицательных чисел

Рациональные числа: ▼

Объединяют в себе все перечисленные выше числа:

• Целые числа
• Дробные числа

Иррациональные числа: ▼

Состоят из:

• Иррациональных положительных чисел
• Иррациональных отрицательных чисел

Действительные числа: ▼

Объединяют в себе все перечисленные выше числа:

• Рациональные числа
• Иррациональные числа

ЦЕЛЫЕ ЧИСЛА

СОСТАВ И ЗАПИСЬ ЦЕЛЫХ ЧИСЕЛ:

Целые числа состоят из:

• Натуральных чисел: 
• Числа ноль: 
• Целых отрицательных чисел: 

Внимание! Число ноль не относится ни к натуральным числам, ни к целым отрицательным числам! Оно само по себе!

Внимание! Натуральные числа иногда называют целыми положительными числами и записывают со знаком плюс:

Но так делают редко и обычно пишут просто    без всякого плюса.

Итак: натуральные числа можно называть целыми положительными числами и записывать, как со знаком плюс, так и без него! Например, между числами и нет никакой разницы: это одно и то же “натуральное число”, или одно и то же “целое положительное число”.

ИЗОБРАЖЕНИЕ ЦЕЛЫХ ЧИСЕЛ:

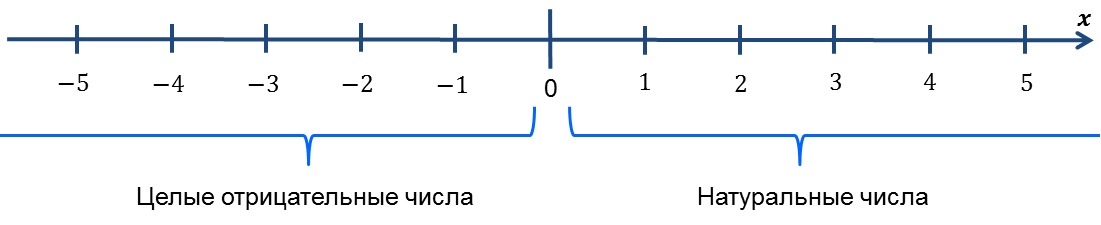
Целые числа очень удобно изображать на прямой линии, так же, как на линейке:

Числовая ось Ox

Такая прямая линия с числами на ней называется числовой осью Ox. Видно, что целые числа расположены слева и справа от нуля, включая и сам ноль.

Изображение целых чисел на числовой оси Ox очень удобно, потому что так их легко сравнивать между собой: чем правее число, тем оно больше. Например, число ноль  больше любого отрицательного числа    потому что оно правее их.

ПРИМЕНЕНИЕ ЦЕЛЫХ ЧИСЕЛ:

Для подсчёта предметов:

• 2 дома, 2-й дом (натуральное число 2);
• 3 книги, 3-я книга (натуральное число 3);
• и другие примеры.

Для записи целых значений различных величин:

• длина 3 метра, 3-й метр (натуральное число 3);
• время 2 часа, 2-й час (натуральное число 2);
• температура 0 градусов (число ноль 0);
• баланс телефона 0 рублей (число ноль 0);
• температура -10 градусов (отрицательное число -10);
• координата -5 метров (отрицательное число -5);
• и другие примеры.

ОПЕРАЦИИ НАД ЦЕЛЫМИ ЧИСЛАМИ:

Над целыми числами можно выполнять различные операции:

• складывать;
• умножать;
• вычитать;
• делить;
• возводить в степень;
• извлекать корень;
• и другие.

ЗАДАЧИ С ЦЕЛЫМИ ЧИСЛАМИ:

Часто встречаемые задачи с натуральными числами:

• сложение, умножение, деление и вычитание натуральных чисел;
• деление с остатком;
• разложение натурального числа на простые множители;
• поиск НОК и НОД;
• задачи на “признаки делимости”;
• возведение натурального числа в степень;
• извлечение корня из натурального числа;
• и другие задачи.

Большинство задач с целыми отрицательными числами учат нас правильно работать со знаками. Например:

• как сложить два отрицательных числа:  
• как умножить два отрицательных числа;  
• как поделить два отрицательных числа:  
• как сложить отрицательное число с натуральным:  
• как извлечь корень из отрицательного числа:  
• и много других подобных задач.

Ещё одна важная задача с целыми числами:

• сравнение целых чисел (см. ниже ▼);

Для решения задач с целыми числами нужно уметь выполнять алгебраические операции: складывать, умножать, делить, вычитать, возводить в степень и др. Например, для “разложения натурального числа на множители” нужно уметь умножать и делить, для “деления с остатком” нужно уметь складывать, умножать, делить и вычитать, а для “сравнения целых чисел” нужно только уметь вычитать. Поэтому, все указанные задачи мы научимся решать после изучения этих операций на странице алгебраические операции в примерах.

ДРОБНЫЕ ЧИСЛА

СОСТАВ ДРОБНЫХ ЧИСЕЛ:

Дробные числа состоят из:

• Дробных положительных чисел (положительные дроби)
• Дробных отрицательных чисел (отрицательные дроби)

ЗАПИСЬ ДРОБНЫХ ЧИСЕЛ:

Дробные числа можно записывать двумя способами:

1-й способ. С помощью обыкновенных дробей:

Вот пример положительных дробей, записанных в виде обыкновенных дробей:

А вот пример отрицательных дробей, записанных в виде обыкновенных дробей:

Подробнее об обыкновенных дробях смотрите ниже ▼.

2-й способ. С помощью конечных десятичных дробей или периодических десятичных дробей:

Вот пример положительных дробей, записанных в виде десятичных дробей (конечных и периодических):

А вот пример отрицательных дробей, записанных в виде десятичных дробей (конечных и периодических):

Подробнее о десятичных дробях смотрите ниже ▼.

Внимание! Положительные дроби можно записывать со знаком плюс:

Но так делают редко и обычно их записывают без знака плюс!

ИЗОБРАЖЕНИЕ ДРОБНЫХ ЧИСЕЛ:

Дробные числа можно изображать на числовой оси Ox. Но обычно сами дробные числа не пишут, потому что они слишком громоздкие, и рисуют вместо них деления, по которым можно приблизительно узнать, где они находятся. Эти деления мы отметили красным цветом:

Числовая ось Ox

Дробные числа расположены между целыми числами. Напомним, что число ноль  относится к целым числам и не является дробным.

Выше мы говорили, что чем правее число, тем оно больше. Поэтому, можно точно сказать, что любая положительная дробь больше любой отрицательной дроби, так как они находятся правее.

Находить местоположение дробных чисел на осях нам пригодится, когда мы будем строить графики различных функций.

ПРИМЕНЕНИЕ ДРОБНЫХ ЧИСЕЛ:

Для записи дробных значений различных величин:

• длина метра;
• объём    литра;
• положительная температура градусов;
• отрицательная температура градусов;
• отрицательная координата метра;
• и другие примеры.

ОПЕРАЦИИ НАД ДРОБНЫМИ ЧИСЛАМИ:

Над дробными числами можно выполнять различные операции:

• складывать;
• умножать;
• вычитать;
• делить;
• возводить в степень;
• извлекать корень;
• и другие.

ЗАДАЧИ С ДРОБНЫМИ ЧИСЛАМИ:

Часто встречаемые задачи с дробными числами:

• сложение, умножение, деление и вычитание обыкновенных и десятичных дробей;
• перевод обыкновенных дробей к десятичным, и наоборот;
• сравнение обыкновенных дробей (см. ниже ▼);
• сравнение десятичных дробей (см. ниже ▼);
• приведение обыкновенных дробей к общему знаменателю;
• перевод неправильных дробей к правильным, и наоборот;
• и много других задач.

Для решения задач с дробными числами нужно уметь выполнять алгебраические операции: складывать, умножать, делить, вычитать, возводить в степень, извлекать корень и др. Например, чтобы “перевести обыкновенные дроби к десятичным, и наоборот” нужно уметь складывать, умножать, делить и вычитать, а чтобы “сравнить обыкновенные дроби” нужно только уметь вычитать. Поэтому, все указанные задачи мы научимся решать после изучения этих операций на странице алгебраические операции и числа.

РАЦИОНАЛЬНЫЕ ЧИСЛА

СОСТАВ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

Рациональные числа – это объединение всех перечисленных выше чисел:

• Целые числа ▲
• Дробные числа ▲

ИЗОБРАЖЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ:

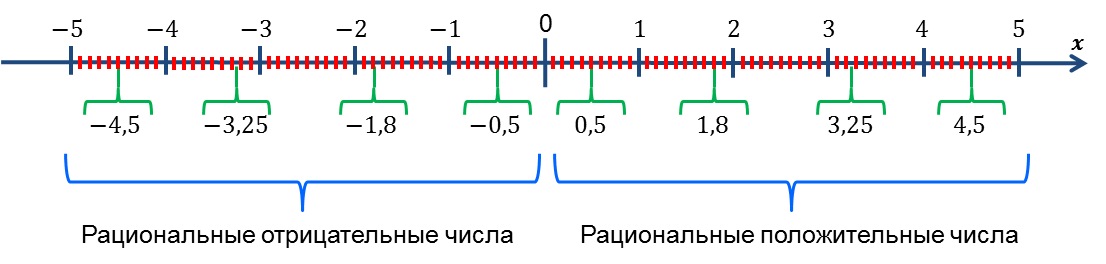
Если на числовой оси Ox изобразить все целые и все дробные числа, то мы получим рациональные числа:

Числовая ось Ox

Под числовой осью мы показали примеры дробных чисел, а над ней – примеры целых чисел. Напомним, что ноль является целым числом, а значит и рациональным числом тоже.

ОПЕРАЦИИ НАД РАЦИОНАЛЬНЫМИ ЧИСЛАМИ:

Смотрите операции над целыми ▲ и дробными ▲ числами.

ЗАДАЧИ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ:

Смотрите задачи с целыми ▲ и дробными ▲ числами.

ИРРАЦИОНАЛЬНЫЕ ЧИСЛА

СОСТАВ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ:

Иррациональные числа состоят из:

• Иррациональных положительных чисел
• Иррациональных отрицательных чисел

ЗАПИСЬ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ:

Иррациональные числа записывают тремя способами:

1-й способ. С помощью бесконечных десятичных дробей:

Вот пример иррациональных положительных чисел, записанных в виде бесконечных десятичных дробей:

А вот пример иррациональных отрицательных чисел, записанных в виде бесконечных десятичных дробей:

Внимание! Бесконечные десятичные дроби нельзя путать с периодическими десятичными дробями, о которых мы писали выше ▲. Вот, сравните их:

• бесконечная десятичная дробь:
  
• периодическая десятичная дробь:
  

Мы видим, что обе дроби являются бесконечными. Однако, у бесконечных десятичных дробей нет периода, то есть повторяющихся комбинаций из цифр. Они не повторяющиеся! Поэтому, давайте запомним: 1) бесконечные десятичные дроби не имеют периода и используются для обозначения иррациональных чисел; 2) периодические десятичные дроби имеют период и используются для обозначения дробных чисел.

2-й способ. С помощью разных операций:

Вот пример иррациональных положительных чисел, записанных с помощью операций:

А вот пример иррациональных отрицательных чисел, записанных с помощью операций:

Это операции извлечения корня    логарифма    синуса    и другие, о которых мы поговорим позже. А сейчас, если у вас есть хороший калькулятор, то попробуйте выполнить эти операции. Вы получите бесконечные десятичные дроби, то есть иррациональные числа. Например:

Согласитесь, что легче оставить иррациональное число в виде операции      или    чем в виде бесконечных десятичных дробей. В этом и есть смысл записывать иррациональные числа в виде операций! Так намного удобнее!

Внимание! Часто, иррациональными числами называют такие записи:

  и другие

Это легко понять! Если    и    являются бесконечными десятичными дробями, то после их сложения, опять получится бесконечная десятичная дробь, то есть иррациональное число! Также, если сложить одно конечное число    и бесконечную десятичную дробь    то всё равно получится бесконечная десятичная дробь, то есть опять иррациональное число!

3-й способ. С помощью специальных символов:

Вот пример иррациональных положительных чисел, записанных с помощью специальных символов:

А вот пример иррациональных отрицательных чисел, записанных с помощью специальных символов:

В школьной алгебре рассматривается всего два таких символа, поэтому их можно запомнить. Это число ПИ    и число Эйлера    Они тоже обозначают иррациональные числа и, поэтому, могут быть записаны в виде бесконечных десятичных дробей:

Внимание! Иррациональные положительные числа можно записывать со знаком плюс:

Но так делают редко и обычно их записывают без знака плюс!

ИЗОБРАЖЕНИЕ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ:

Иррациональные числа можно изображать на числовой оси Ox. Для этого, сначала нужно записать их в виде бесконечных десятичных дробей, а потом уже приблизительно найти их местоположение на оси. Давайте, например, узнаем местоположение положительных и отрицательных иррациональных чисел  Сначала представим их в виде бесконечных десятичных дробей:

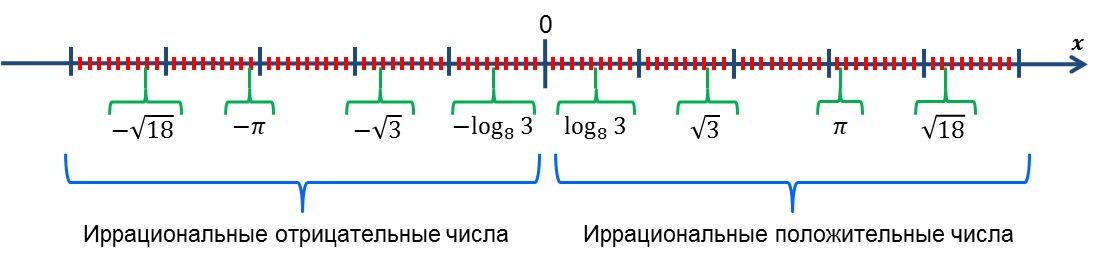
А теперь можно приблизительно найти их местоположение (положительные числа мы записали без знака плюс):

Числовая ось Ox

Напомним, что число ноль  относится к целым числам и не является иррациональным.

Выше мы говорили, что чем правее число, тем оно больше. Поэтому, можно точно сказать, что любое иррациональное положительное число больше любого иррационального отрицательного числа, так как они находятся правее.

Находить местоположение иррациональных чисел на осях нам пригодится, когда мы будем строить графики различных функций. Смотрите, например, страницу алгебраические функции.

ПРИМЕНЕНИЕ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ:

В повседневном быту иррациональные числа практически не встречаются. Вспомните, часто ли вы слышите слова: “С вас рублей!”? Иррациональные числа чаще всего применяются в научной или инженерной деятельности. Там часто приходится пользоваться операциями извлечения корня, логарифма, синуса, косинуса и т.д., которые, как вы уже знаете, как раз и приводят к иррациональным числам. Поэтому, главное применение иррациональные числа находят именно в этих областях.

ОПЕРАЦИИ НАД ИРРАЦИОНАЛЬНЫМИ ЧИСЛАМИ:

Над иррациональными числами можно выполнять различные операции:

• складывать;
• умножать;
• вычитать;
• делить;
• возводить в степень;
• извлекать корень;
• и другие.

ЗАДАЧИ С ИРРАЦИОНАЛЬНЫМИ ЧИСЛАМИ:

Часто встречаемые задачи с иррациональными числами:

• сложение, умножение, деление и вычитание иррациональных чисел;
• сравнение иррациональных чисел (см. ниже ▼);

Выше, мы показали, что иррациональные числа можно записывать с помощью операций извлечения корня    логарифма    синуса    и других. Поэтому, решать указанные задачи, мы будем после изучения данных операций. Смотрите страницы алгебраические операции в примерах, тригонометрические операции в примерах, логарифмические операции в примерах, показательные операции в примерах.

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА

СОСТАВ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ:

Действительные числа – это объединение всех перечисленных выше чисел:

• Рациональные числа ▲
• Иррациональные числа ▲

ИЗОБРАЖЕНИЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ:

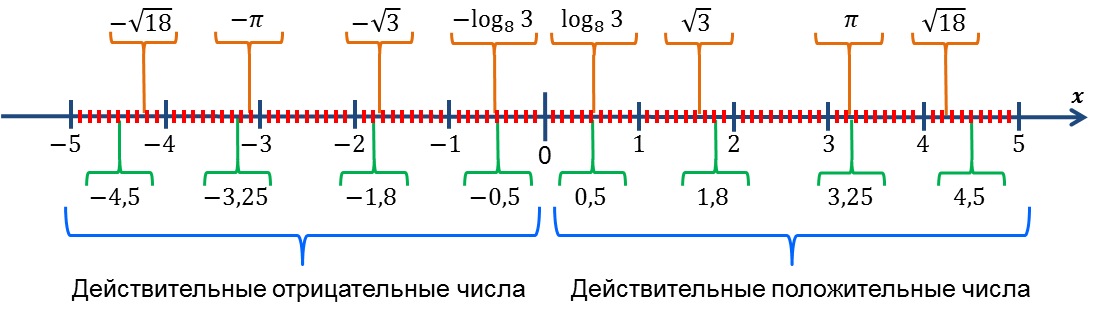
Если на числовой оси Ox изобразить все целые, дробные и иррациональные числа, то мы получим действительные числа. Они охватывают всю ось, каждую её точку, от минус бесконечности, до плюс бесконечности:

Числовая ось Ox

Под числовой осью мы показали примеры дробных чисел, посередине – целых, а над ней – иррациональных.

ОПЕРАЦИИ НАД ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ:

Смотрите операции над целыми ▲, дробными ▲ и иррациональными ▲ числами.

ЗАДАЧИ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ:

Смотрите задачи с целыми ▲, дробными ▲ и иррациональными ▲ числами.

СРАВНЕНИЕ ЧИСЕЛ. ЗНАКИ СРАВНЕНИЯ

В доработке!!!

ЧИСЛОВЫЕ ПРОМЕЖУТКИ

В доработке!!!

ДОПОЛНИТЕЛЬНО

ПОДРОБНЕЕ ОБ ОБЫКНОВЕННЫХ ДРОБЯХ

Выше мы написали, что обыкновенные дроби – это один из способов записи дробных чисел, и показали несколько примеров обыкновенных дробей. А теперь, давайте поговорим о них поподробнее.

Обыкновенные дроби – это дробные числа, записанные в виде:

где – числитель, – знаменатель. Например:

Внимание! Обыкновенные дроби    получили своё происхождение от операции деления. Например, дробь    означает один поделить на два    Попробуйте выполнить это на калькуляторе. Результатом будет число    то есть десятичная запись данной дроби. Вспомните также школу! Там нас учили, что дроби получаются после деления тортов, яблок и прочих предметов на части, и эти части мы называли одна вторая    торта, одна третья    торта и т.д. Итак, давайте запомним: обыкновенные дроби совпадают с операцией деления! В будущем, нам это сильно пригодится для решения разных задач с дробными числами. В частности, для перевода обыкновенных дробей в десятичные нужно будет делить числитель    на знаменатель  .

Те дроби, у которых числитель меньше знаменателя называются правильными:

А те дроби, у которых числитель    больше знаменателя    называются неправильными:

Из неправильных дробей можно перейти к правильным, но в этом случае у них появится целая часть (такие дроби называются смешанными):

где   – это целая часть дроби,  при этом    станет меньше  .  Например:

Для перевода неправильных дробей к правильным (и наоборот), нужно уметь выполнять алгебраические операции сложения, умножения, деления и вычитания. Поэтому, указанную задачу мы научимся решать после изучения этих операций на странице алгебраические операции и числа.

ПОДРОБНЕЕ О ДЕСЯТИЧНЫХ ДРОБЯХ (КОНЕЧНЫХ И ПЕРИОДИЧЕСКИХ):

Выше мы написали, что десятичные дроби – это один из способов записи дробных чисел, и показали несколько примеров десятичных дробей. А теперь, давайте поговорим о них поподробнее.

Все конечные десятичные дроби имеют вид:

где  – целая часть дроби,   – дробная часть дроби. Примеры конечных десятичных дробей:

Все периодические десятичные дроби имеют вид:

где  – целая часть дроби,   – дробная часть дроби,  – период дроби. Примеры периодических десятичных дробей:

Видно, что период бесконечно повторяется!!!